几何教学是初中数学教学的难点也是重点，几何复习课更是重中之重。此次疫情我们有幸借助空中课堂，聆听了几位大咖的几何复习课，不仅是学生听的津津有味，我们老师也是竖起耳朵仔细听大咖老师们的每一个措辞、过渡语，回味无穷。下面我就通过空中课堂的两节几何复习课，谈谈我的一些所思所想，以及我是怎么落实到我的初三几何教学中的。

第一位“巨人”是浦东新区数学教研员齐老师，齐老师的课让我对几何复习教学有了更深的理解。这是《等腰三角形与直角三角形、全等三角形》复习课中的一个精彩片段：

例题1：已知：如图，在△ABC中，AB=2AC，∠A=60°。求证：AC⊥BC。

齐老师先从结论进行分析：证明垂直的最基本的方法有哪些？

（1）从定义出发证夹角为90°；

（2）在一个三角形中可以用勾股定理的逆定理。 

当然除了这两种方法还有其他证明两直线垂直的方法，掌握的越多越有利于找到合适的方法解决问题。

接着再从条件分析：

注意到“AB=2AC：倍半关系”，采用“截长补短”法，可以“截长”也可以“补短”；

注意到“∠A=60°：特殊角”构造直角三角形。

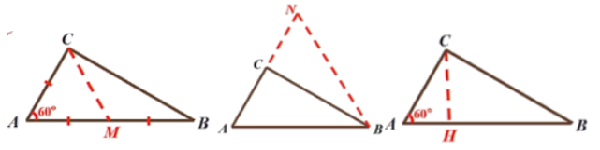
不难发现审题人的着眼点不同，添辅助线的方法也不同，但是不变的是分析题目的方法。

齐老师通过对结论和条件的分析，帮助学生们精准地找到添辅助线的方法，突破了这道题的难点。

启示：几何教学中，添正确的辅助线一直是学生的难点，也是解题的重点。须教会学生执果索因，从要解决的问题，联想所学知识，考虑添置合适的辅助线。

第二位“巨人”是黄浦区数学教研员顾老师，他的几何复习课以自身为切入点，与学生们娓娓道来，现身说法自己的解题经验。他的《相似三角形（1）》中印象最深的一个片段是例题的讲解：

例题2：如图，BD是△ABC边AC上的中线，点G是其重心，点E是线段GD的中点，联结CE并延长交边AB于点F。求AF:FB。

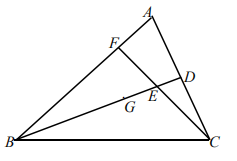
顾老师先介绍了自己在解题时的做法：

从结论着手分析，要证线段的比，想到利用三角形一边的平行线性质进行传递

通过分析发现是可以的。

通过添辅助线，来“筑路”构造基本型。怎么添？

可以过点D作AB的平行线，问题很简单就解决了。

但是顾老师站在学生的角度进行考虑，预想学生在解题时：

更喜欢添水平线的平行线

两种方法进行比较，不难发现，第一种方法更简单。第一种方法是直接传递，第二种方法是间接传递。

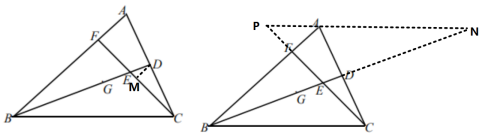
由此学生体会到线段比的传递需要基本型，线段比的传递是有方向感的，选择好的方向事半功倍。

启示：顾老师能够站在学生的立场，想学生所想，将学生的想法和做法作为课堂的主要内容进行展示，通过几种方法的比较，不仅拓宽了学生的思维，更帮助学生找到了几种方法差异的本质，学生也能够通过学习及时发现自己解题时的问题并能够调整策略。在这样一次次地分析过程中也磨砺了学生，培养了学生的探究数学的品质。

通过观摩两位“巨人”老师的几何复习课，

我学会了在几何教学中，教会学生对于证明问题，应当从条件想可知，从未知想需知，并将自己的思维过程写下来，能够有序地思考问题；

学会了要站在学生的角度进行备课，充分挖掘一道题目的多种解法，预设到学生会遇到哪些困难，以学生为主体进行教学设计。

从模仿“巨人”老师开始。在作业讲评中关注挖掘学生的解题思路，比如等腰三角形与直角三角形、全等三角形作业单中第7题：

已知：如图，在四边形ABCD中，∠A=90°，BD=DC,BC=2AB.求证：点D在∠ABC的平分线上。

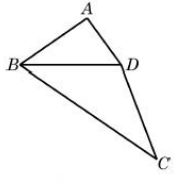
在作业讲评课时提问学生为什么这么添辅助线，主要的着眼点是什么？让学生模仿齐老师的分析方法回答，帮助总结方法：

1、注意到“等腰”，考虑“添底边上的高、中线、顶角平分线”的方法；

2、注意到“倍半关系”，考虑“截长补短”法；

3、注意到“角平分线”，考虑添另一边的高。

从而帮助学生从结论、条件着手分析，添置合适的辅助线。

通过几次的磨练，学生们的几何分析能力确实得到了提升，对于一些有难度的题目也能够抓住题目条件或者结论的着眼点进行分析，最终找到合适的方法。

在平时的习题讲评课时，我也鼓励学生像齐老师、顾老师一样将自己的思维过程写下来，通过批改作业了解学生方法的差异，挖掘学生们的一题多解，进行展示，也会展示学生错误的过程，一起讨论错在哪里，是哪一步的分析出现了错误，应该怎么进行修改。然后请学生一起比较几种方法，提炼通性通法，总结出解题策略。